Реальные возможности для наиболее полной автоматизации фотограмметрических процессов Заключаются в комплексном использовании ЭВМ и устройств ввода изображений в ЭВМ. При стереофотограмметрических работах важнейшей задачей является автоматическая идентификация на аэрофотоснимках стереопары соответственных точек. Оптимальное решение ее необходимо для эффективной реализации большинства автоматизированных технологий получения данных о местности по стереопаре аэрофотоснимков.
В настоящей статье анализируются свойства образов точек цифровых снимков, используемых при автоматической идентификации, и предлагаются критерии для их оценки.
Цифровым снимком (ЦС) будем называть цифровое отображение какого-либо снимка [4], записанное на машинном носителе информации. Топографический ЦС, следовательно, есть записанное на машинном носителе информации цифровое отображение топографического фотоснимка центральной проекции, т. е. результат цифрования исходного фотоизображения. Аналогично можно сформулировать понятия «телевизионный ЦС», «радиолокационный ЦС» и т. д. [4]. Цифровой снимок Р может быть представлен в виде множества
![]()
где хi уi. — координаты i-й точки исходного снимка; а1i, а2i, ., аni; — параметры, описывающие свойства i-й точки исходного снимка или некоторой области, включающей эту точку.
Под участком ЦС будем понимать подмножество С множества Р, причем их размеры т(Р) и т(С) таковы, что т (Р)>> т (С).
Образом точки хi уi назовем множество О, включающее точку хi уi в качестве его центральной точки. Образ точки может быть непосредствен¬но участком исходного ЦС или его можно получить путем преобразова¬ния такого участка, т. е.
![]()
В наиболее простом случае изображение аэрофотоснимка в результате цифрования представляют в виде матрицы значений оптических плотностей d
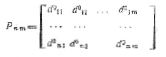
каждый элемент которой отнесен к узлу i, j регулярной сетки дискретизации. Образом точки ЦС в данном случае является матрица
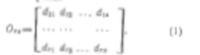
такая, что
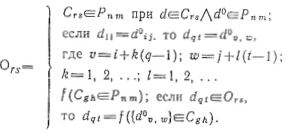
Автоматическую цифровую идентификацию точек стереопары ЦС осуществляют путем сличения образов точек О и О' первого и второго ЦС [1, 5]. При этом обычно вычисляют взаимную корреляционную функцию текущих образов О и О' и по ее максимуму принимают решение о совпадении образов.
Существенно упростить схему вычислений позволяет применение релейных и полярных корреляционных функций [3]. При этом более острый пик этих функций обеспечивает большую точность определения их максимума. Применение релейных и полярных корреляционных функций предполагает клиппировапие исходного сигнала, т. е. его замену знакопеременным сигналом постоянной амплитуды. Амплитуду клиппированиого сигнала можно при желании изменять, регулируя таким образом крутизну характеристик и чувствительность метода.
Однако переход от обычных корреляционных функций к релейным и полярным приводит к появлению методической ошибки, вызванной заменой исходного сигнала клиппированным. Очевидно, значение этой ошибки зависит от степени подобия сигналов.
Можно сделать вывод, что при сходстве форм исходных и клиппированных сигналов надежность определения максимума взаимной корреляционной функции повышается. В фотограмметрическом смысле поставленному условию в наибольшей степени могут удовлетворять изображения так называемых четких контуров. Для выявления степени приближения образов точек к изображениям четких контуров необходим специальный анализ образов О.
Оценка образов точек ЦС может быть выполнена с использованием известных статистических критериев [3]. Так, автокорреляционная функция — математическое ожидание произведений значений оптической плотности в двух точках образа — позволяет получить средний размер деталей образа, определяющих его структуру, выявить периодичность изменения оптических плотностей образа. Аналогичные свойства изображения выявляются с помощью структурной функции, представляющей собой математическое ожидание квадрата разности оптических плотностей в двух текущих точках образа. Значение модуля градиента оптической плотности характеризует пространственную скорость изменения ее в образе точки.